一维无过程噪声的卡尔曼滤波
我们知道,估计值的不确定性很容易得到,因为我们只需要等到下一个时刻的测量值出来,计算方差就可以了。但是,不能忽略的还有测量误差,或称测量的不确定性,用高中物理的话说,系统误差。度量测量误差的量是方差。需要注意的是,状态估计的方差也应当进行外插。
这里再重复一下外插,GPT给出的解释是,利用当前时刻的状态估计和系统模型,对下一时刻的状态进行预测。这一步是基于状态转移方程完成的。状态转移方程描述了系统状态如何随时间变化。说白了,外插就是你根据刚刚得到的测量值和已有的规律对下一时刻进行的预测。
那么,状态估计的方差应当如何外插?在上一篇第一个事例里,金条的重量是固定的。此时方差显然不变,有:
在第二个例题里,方差可以这样外插,其中$p^x$是位置估计的方差:
\[p^x_{n+1,n}=p^x_{n,n}+\Delta t^2 \cdot p^v_{n,n}\] \[p^v_{n+1,n}=p^v_{n,n}\] 这里显然有一个疑问,为什么第一个方程外插的方差是乘以时间的平方?
定理:对于任何服从于方差$\sigma^2$的正态分布随机变量x,kx服从方差$k^2\sigma^2$的正态分布。所以后面一项会变成t平方。
卡尔曼滤波器是一种最优滤波器,最优性体现在它能够把上述状态预测和测量值融合在一起,使得得到的当前状态估计不确定性最小。当前状态估计值是状态预测和测量值的加权和:
\[\hat{x}_{n,n}=w_1z_n+w_2\hat{x}_{n,n-1}\] \[w_1+w_2=1\]那么:
\[\hat{x}_{n,n}=w_1z_n+(1-w_1)\hat{x}_{n,n-1}\]没错,这是废话。那么,方差如下给出,其中$r_n$是测量值$z_n$的方差,$p_{n,n-1}$ 是状态预测值$\hat{x}{n,n-1}$ 的方差, $p{n,n}$是最优估计$\hat{x}_{n,n}$的方差:
\[p_{n,n}=w^2_1r_n+(1-w_1)^2p_{n,n-1}\]我们试图找到一个最优估计使得最小化$p_{n,n}$,为了能找到最小化$p_{n,n}$的$w_1$,我们把$p_{n,n}$对$w_1$求导,并令导数等于零:
\[\frac{dp_{n,n}}{dw_1}=2w_1r_n-2(1-w_1)p_{n,n-1}=0\] \[2w_1r_n=2(1-w_1)p_{n,n-1}\] \[w_1r_n=p_{n,n-1}-w_1p_{n,n-1}\] \[w_1=\frac{p_{n,n-1}}{p_{n,n-1}+r_n}\]此时的$w_1$又称卡尔曼增益$K_n$,将其代入状态估计方程:
\[\begin{aligned} \hat{x}_{n,n} &= w_1z_n+(1-w_1)\hat{x}_{n,n-1} \\ &= w_1z_n+\hat{x}_{n,n-1}-w_1\hat{x}_{n,n-1} \\ &= \hat{x}_{n,n-1} + w_1(z_n - \hat{x}_{n,n-1}) \\ \hat{x}_{n,n} &= \hat{x}_{n,n-1} + \frac{p_{n,n-1}}{p_{n,n-1}+r_n}(z_n - \hat{x}_{n,n-1}) \end{aligned}\]最后一个方程称为卡尔曼增益方程,一维情况下,卡尔曼增益具有如下的形式:
\[K_n=\frac{预测值的方差}{预测值的方差+测量值的方差}=\frac{p_{n,n-1}}{p_{n,n-1}+r_n}\] 这下看懂了,原来这个式子竟然是令方差最小求导得到的。我曾阅读过许多博客,有人认为这个式子是从概率论中的不确定性得到的,是一种不确定性的更新。这个理解我觉得也很好,比较符合客观实践的直觉,但是我当时比较蠢没看懂。现在我们使用简单的导数就得到了这个式子,虽然从方差的角度来看,好像并不是很直觉,但是我却觉得反而更好理解了呢?
回到刚刚的讨论,卡尔曼增益系数是一个0到1之间的数(这个是显然的)。我们推导一下状态估计的方差:
我们希望方差也是递推形式的,所以:
\[\begin{aligned} p_{n,n} &= (\frac{p_{n,n-1}}{p_{n,n-1}+r_n})^2r_n+(\frac{r_n}{p_{n,n-1}+r_n})^2p_{n,n-1} \\ &= \frac{p_{n,n-1}r_n}{p_{n,n-1}+r_n}(\frac{p_{n,n-1}}{p_{n,n-1}+r_n}+\frac{r_n}{p_{n,n-1}+r_n}) \\ &= (1-K_n)p_{n,n-1}(K_n+1-K_n) \\ &= (1-K_n)p_{n,n-1} \end{aligned}\]该方程更新了状态估计的方差,称之为协方差更新方程。并且,因为$(1-K_n)<1$,协方差是在不断下降的,也就是说,不确定性是在逐渐下降的。卡尔曼增益描述的是当前量测值的置信度。代表你有多大程度相信当前的量测值。当你认为当前量测的十分不准时,卡尔曼增益很低,状态估计收敛速度很慢;当你十分确定当前量测的时候,卡尔曼增益很高,状态估计将会快速收敛。
总结
算法流程:首先,滤波器初始化,提供两个参数:初始状态$\hat{x}{0,0}$和初始的不确定性(初始状态方差)$p{0,0}$ 。说方差可能难以理解,例如,飞机的初始距离是1wm,你的雷达误差是100m,那么标准差就是100,方差是10000.
测量:每次测量得到两个参数:测量值 $z_n$ 和测量方差 $r_n$ ,滤波器输出为状态估计 $\hat{x}{n,n}$ 和状态估计方差 $p{n,n}$
所有方程列出如下,前三个方程是状态更新阶段,或者说状态估计阶段,用于估计当前的状态。后六个方程是用于预测的。
卡尔曼增益方程 (Kalman Gain):
\[K_{n} = \frac{p_{n,n-1}}{p_{n,n-1}+r_{n}}\]状态更新方程 (State Update):
\[\hat{x}_{n,n} = \hat{x}_{n,n-1}+ K_{n} \left( z_{n}- \hat{x}_{n,n-1} \right)\]协方差更新方程 (Covariance Update):
\[p_{n,n} = \left( 1-K_{n} \right) p_{n,n-1}\]恒定动态模型下,状态外插 (State Extrapolation) 方程:
\[\hat{x}_{n+1,n}= \hat{x}_{n,n}\]速度恒定动态模型下,状态外插 (State Extrapolation) 方程:
\[\hat{x}_{n+1,n}= \hat{x}_{n,n}+ \Delta t\hat{\dot{x}}_{n,n}\] \[\hat{\dot{x}}_{n+1,n}= \hat{\dot{x}}_{n,n}\]恒定动态模型下,协方差外插 (Covariance Extrapolation) 方程:
\[p_{n+1,n}= p_{n,n}\]速度恒定动态模型下,协方差外插 (Covariance Extrapolation) 方程:
\[p_{n+1,n}^{x}= p_{n,n}^{x} + \Delta t^{2} \cdot p_{n,n}^{v}\] \[p_{n+1,n}^{v}= p_{n,n}^{v}\]从另一个角度看状态更新方程:
\[\hat{x}_{n,n} = \hat{x}_{n,n-1}+ K_{n} \left( z_{n}- \hat{x}_{n,n-1} \right)=\left(1-K_n\right)\hat{x}_{n,n-1}+K_nz_n\]可见,卡尔曼增益$K_n$是当前测量值$z_n$的权重,$1-K_n$是当前状态预测的权重。卡尔曼增益高的时候,代表你更相信测量,那么新的状态估计值会更接近测量值;相反,则会更接近估计值。
考虑过程噪声
考虑这样的情形:我们想要测量一个电阻的阻值,很显然电阻的阻值应当是不变的,但是也难免会随着温度有微小的变动;某架飞机正在匀速巡航,但是也难免会有突然的加速减速之类。这种噪声统一称之为过程噪声。在之前的估计里,我们认为匀速运动的物体完美遵守匀速运动的定义,这里,我们不妨将过程噪声考虑进去。
过程噪声方差用$q$表示,协方差外插方程应当包含过程噪声,那么,恒定动态模型的协方差外插方程为:
速度恒定动态模型的协方差外插方程为:
\[p_{n+1,n}^{x}= p_{n,n}^{x} + \Delta t^{2} \cdot p_{n,n}^{v}\] \[p_{n+1,n}^{v}= p_{n,n}^{v} + q_n\]跟踪过程的稳态误差
可能是动态模型阶数低于实际动态模型的阶数。例如明明是一个线性增长的模型,动态模型却假设为静止的,这样就会造成稳态误差。
解决办法除了更新动态模型,还可以调大过程噪声的协方差。这样滤波器就会更加相信测量值,而不是预测值。但是这样其实就达不到滤波的效果了。如果测量值准确还好,不准确就完全没办法处理了。
不过,实际上,本来也很难对一个东西进行动态模型的描述,例如巡航的飞机,难免会有大大小小的加速度,建模是不可能完全对其描述的,过程噪声就是很大!在我的理解,过程噪声虽然名叫噪声,实际上算是一个调节因子,合理的设置过程噪声能让你的模型更加准确。
多维卡尔曼滤波的基础知识
方差和期望的基本性质
方差和期望的关系:
\[D(X) = E(X^{2}) - E^2(X)\]协方差的展开:
\[COV(X,Y) = E(XY) - E(X)E(Y)\] \[COV(X,Y) = E[(X-\mu_x)(Y-\mu_y)]\]当X和Y相互独立的时候:
\[COV(X,Y) = 0\]方差的展开:
\[D(X \pm Y) = D(X) + D(Y) \pm 2COV(X,Y)\]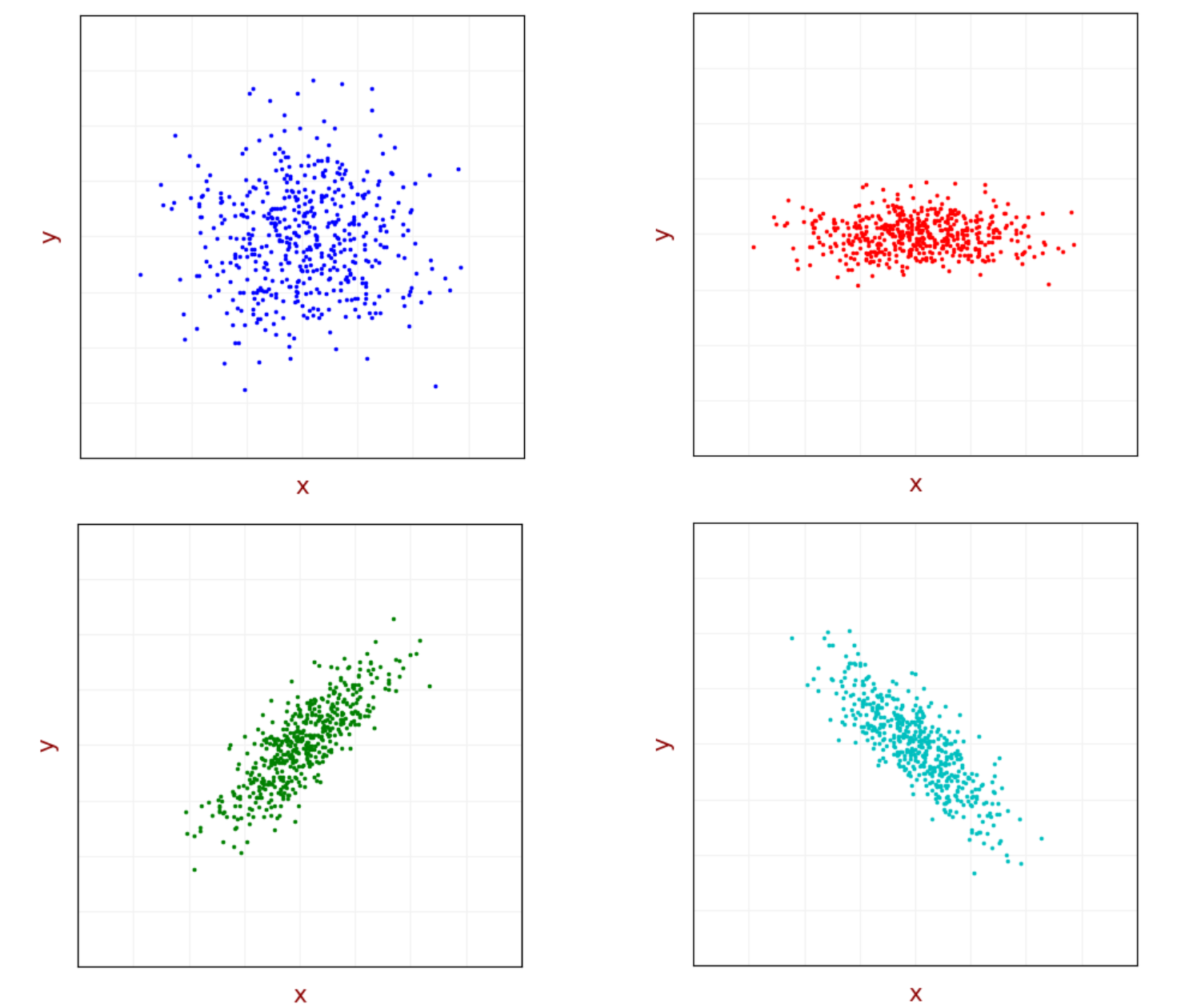
左上的图中,X和Y的方差是相等的,并且取值并不互相依赖,右上虽然看起来有规律,其实并不是。它只是Y的方差比X的小,X和Y仍然不具有相关性。因为你这么看,对于任意的一个X,Y的取值十分多样。
下面的两张图都是XY相关的分布。绿色图中,X越大,Y也越大,所以具有相关性,并且协方差是正的。青色的图翻过来,X越大Y越小,协方差是负的。
对于具有N个样本的总体,协方差计算公式如下,总体的意思是,你能统计到这个总体的每一个元素,或者称全量样本:
当从总体中取N个样本进行考察的时候:
\[COV(X,Y) = \frac{1}{N-1}\sum_{i=1}^{N}(x_{i} - \mu_{x})(y_{i} - \mu_{y})\]公式2,这个只是对上面那个变换了一下:
\[COV(X,Y) = \frac{1}{N-1}\sum_{i=1}^{N}(x_{i}y_{i}) - \frac{N}{N-1}\mu_{x}\mu_{y}\] 这个和方差的计算有点相似哈,都是除以N-1来归一化。除以什么关键看你得到的究竟是样本,还是整个总体。
协方差矩阵
下面讨论协方差矩阵。协方差矩阵是一个方阵,描述一系列随机变量两两之间的协方差。对于一个二维随机变量,协方差矩阵为:
\[\boldsymbol{\Sigma} =\left[ \begin{matrix}\sigma_{xx} & \sigma_{xy} \\ \sigma_{yx} & \sigma_{yy} \\ \end{matrix} \right] = \left[ \begin{matrix} \sigma_{x}^{2} & \sigma_{xy} \\ \sigma_{yx} & \sigma_{y}^{2} \\ \end{matrix} \right] = \left[ \begin{matrix} VAR(\boldsymbol{x}) & COV(\boldsymbol{x, y}) \\ COV(\boldsymbol{y, x}) & VAR(\boldsymbol{y}) \\ \end{matrix} \right]\]注意该矩阵中的非对角元素是相等的,因为$COV(\boldsymbol{x, y}) = COV(\boldsymbol{y, x})$ ,如果XY是相互独立的,那么非对角元素是0,因为此时$COV(X,Y) = 0$。对n维随机变量,其协方差矩阵为:
\[\boldsymbol{\Sigma} = \left[ \begin{matrix} \sigma_{1}^{2} & \sigma_{12} & \cdots & \sigma_{1n} \\ \sigma_{21} & \sigma_{2}^{2} & \cdots & \sigma_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{n1} & \sigma_{n2} & \cdots & \sigma_{n}^{2}\\ \end{matrix} \right]\]协方差矩阵的性质:
- 协方差矩阵的对角元素即为每个多维随机变量分量的方差。这是显然的,我们从公式就能看到。
- 由于对角元素非负,协方差矩阵的迹(对角元素之和)也非负。
- 协方差矩阵是对称阵。因为$COV(X,Y)=COV(Y,X)$
- 协方差矩阵是半正定矩阵。如果对于任何向量$v\neq0$,都有$\boldsymbol{v}^{T}\boldsymbol{A}\boldsymbol{v} \geq 0$,则矩阵 A 称为半正定矩阵。A 的特征值均为非负。
定理:给定一个有 k 个元素的向量 x :
\[\boldsymbol{x} = \left[ \begin{matrix} x_{1}\\ x_{2}\\ \vdots \\ x_{k}\\ \end{matrix} \right]\]x 的协方差矩阵为:
\[COV(\boldsymbol{x}) = E \left( \left( \boldsymbol{x} - \boldsymbol{\mu}_{x} \right) \left( \boldsymbol{x} - \boldsymbol{\mu}_{x} \right)^{T} \right)\]证明:
\[COV(\boldsymbol{x}) = E \left( \left[ \begin{matrix} (x_{1} - \mu_{x_{1}})^{2} & (x_{1} - \mu_{x_{1}})(x_{2} - \mu_{x_{2}}) & \cdots & (x_{1} - \mu_{x_{1}})(x_{k} - \mu_{x_{k}}) \\ (x_{2} - \mu_{x_{2}})(x_{1} - \mu_{x_{1}}) & (x_{2} - \mu_{x_{2}})^{2} & \cdots & (x_{2} - \mu_{x_{2}})(x_{k} - \mu_{x_{k}}) \\ \vdots & \vdots & \ddots & \vdots \\ (x_{k} - \mu_{x_{k}})(x_{1} - \mu_{x_{1}}) & (x_{k} - \mu_{x_{k}})(x_{2} - \mu_{x_{2}}) & \cdots & (x_{k} - \mu_{x_{k}})^{2} \\ \end{matrix} \right] \right) =\] \[= E \left( \left[ \begin{matrix} (x_{1} - \mu_{x_{1}}) \\ (x_{2} - \mu_{x_{2}}) \\ \vdots \\ (x_{k} - \mu_{x_{k}}) \\ \end{matrix} \right] \left[ \begin{matrix} (x_{1} - \mu_{x_{1}}) & (x_{2} - \mu_{x_{2}}) & \cdots & (x_{k} - \mu_{x_{k}}) \end{matrix} \right] \right) =\] \[= E \left( \left( \boldsymbol{x} - \boldsymbol{\mu}_{x} \right) \left( \boldsymbol{x} - \boldsymbol{\mu}_{x} \right)^{T} \right)\]协方差椭圆
协方差椭圆是高斯分布的一条特殊等高线,使我们能以二维形式展示 1σ 置信区间,从而从几何角度直观解释协方差矩阵。
任何椭圆可以由四个参数描述:椭圆圆心坐标$\mu_x\mu_y$,半长轴a,半短轴b,朝向角$\theta$。
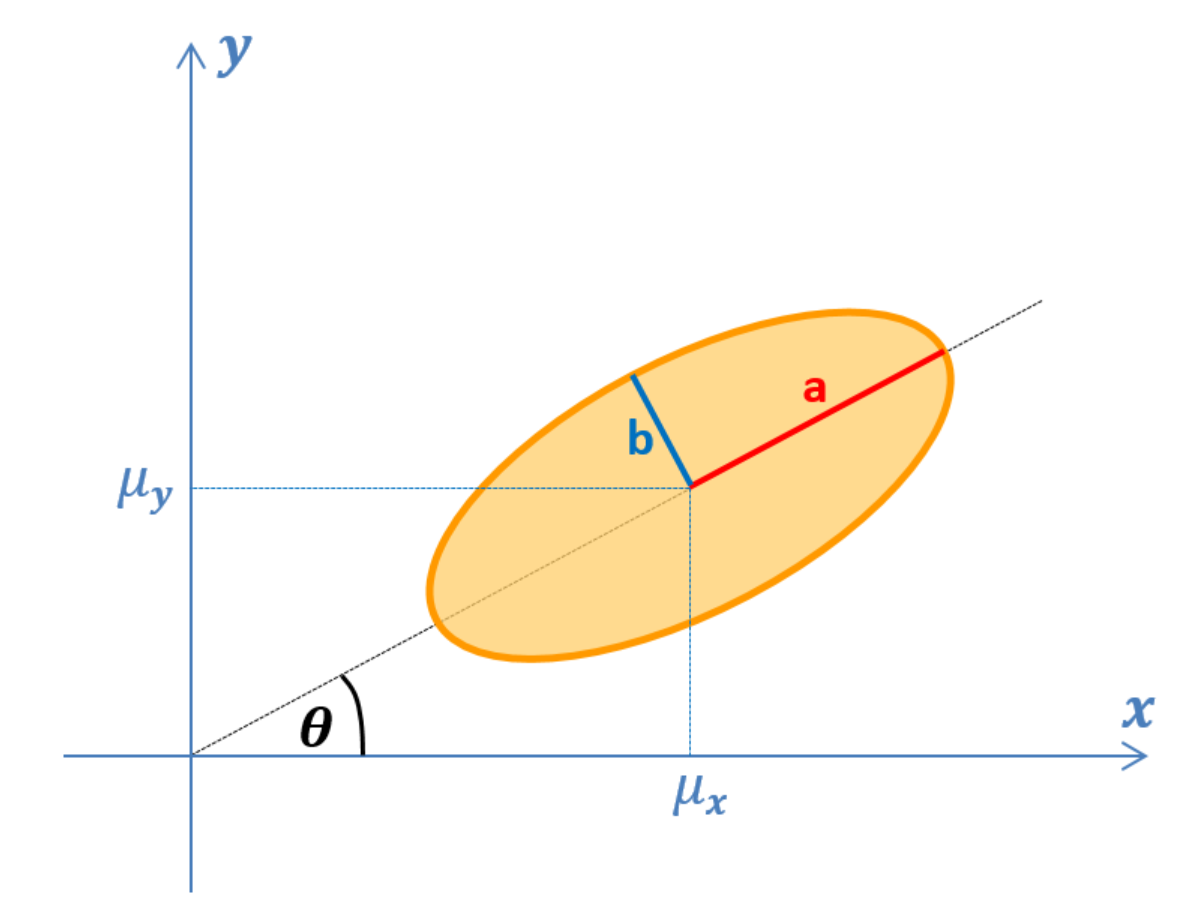
椭圆心是随机变量的均值:
\[\mu_{x} = \frac{1}{N}\sum^{N}_{i=1}x_{i}\] \[\mu_{y} = \frac{1}{N}\sum^{N}_{i=1}y_{i}\]椭圆半长轴和半短轴长度是对应随机变量协方差矩阵的特征值的平方根:
- 半长轴长度 a 是最大的特征值平方根
- 半短轴长度 b 是第二大的特征值的平方根
椭圆的朝向由随机变量协方差矩阵的特征向量给出:
\[\theta = arctan \left( \frac{v_{x}}{v_{y}} \right)\]式中:
- vx 是协方差矩阵对应最大特征值的特征向量的 x 分量
- vy 是协方差矩阵对应最大特征值的特征向量的 y 分量
