当记忆的线缠绕过往支离破碎,是慌乱占据了心扉。—-《寂寞沙洲冷》
超前进位加法器原理
1. 一位二进制的加法
首先考虑两个1位二进制相加 a+b,不考虑上一级的进位,0和1简单相加,即使是三岁小孩理解下面的表格想必也没有什么困难
| 上一级的进位(Cn-1) | A | B | 进位(Cn) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
结论显而易见,A&B==1(AB=1)的时候存在进位
2. 考虑存在输入的进位情况下的进位:
| 上一级的进位(Cn-1) | A | B | 进位(Cn) |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
那么,考虑上一级进位的情况下,A or B==1(A+B=1)时存在进位
3. 卡诺图公式推导
用到一点简单的数电知识,综合以上两个表格,画出卡诺图如下:
一位挂科的学生默默翻开了书复习卡诺图化简
| C[n-1]\AB | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
短暂复习过后,不难看出,存在三个圈,则根据卡诺图写出最简表达式为:
逻辑表达式为:
C[n] = AB + BC[n-1] + AC[n-1]
= AB + C[n-1](A + B)
使用逻辑运算符书写为:
C[n] = (A[n] & B[n]) || ((A[n] || B[n]) & C[n-1])
即使你没有挂科,如果不会,请去看看数电书。
4.超前进位递推式
既然递推式得到了,那么事情就变得简单了。例如: 设两个八位二进制加数为A、B,则:
C0 = A[0] || B[0] (第一位没有上一级的进位)
C1 = (A[1] & B[1]) || ((A[1] || B[1]) & C[0])
C2 = (A[2] & B[2]) || ((A[2] || B[2]) & C[1])
C3 = (A[3] & B[3]) || ((A[3] || B[3]) & C[2])
C4 = ······
5. 二进制本位加法
两个一位二进制数相加忽略之前的进位,其
ans = A xor B
考虑之前的进位,设进位为C[n-1],二进制数为A、B,则:
| C[n-1] | A | B | ans[n] |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
这次,聪明的你想必不需要卡诺图也能直接看出来表达式了,没错,就是:
ans[n] = C[n-1] xor (A[n] xor B[n])
6. 总结
设两加数为A、B,且进位数组为C[n],答案为ans[n],则:
C[0] = A[0] & B[0];
ans[1] = A[0] xor B[0];
C[1] = (A[1] & B[1]) || ((A[1] || B[1]) & C[0]);
ans[2] = C[1] xor (A[2] xor B[2]);
C[2] = (A[2] & B[2]) || ((A[2] || B[2]) & C[1]);
ans[3] = C[2] xor (A[3] xor B[3]);
······
7.代码
根据上述分析,使用verilog写出四位超前进位加法器如下: (这样写真的很蠢,不要这样写,别的博主有写的更好的,这里贴一篇。他的代码很简单美观。但是注意到他这篇文章的评论有人说他写的不是超前进位,好像确实是这样,因为他那个本质还是递推) 需要注意的是, 超前进位加法器的本质是用电路的复杂程度去换时间。–《数字电子技术基础(第六版)》
module top(
input [3:0] a,
input [3:0] b,
input c,
output [3:0] ans
);
wire [3:0] C;
assign ans[0] = a[0] ^ b[0];
assign C[0] = a[0] & b[0];
//这些注释掉的都是递推式,你可以先写好递推式再把上面的C[n-1]复制粘贴替换进去就可以
//assign ans[1] = C[0] ^ (a[1] ^ b[1]);
//assign C[1] = ((a[1] | b[1]) & C[0]) | (a[1] & b[1]);
assign ans[1] = (a[0] & b[0]) ^ (a[1] ^ b[1]);
assign C[1] = ((a[1] | b[1]) & (a[0] & b[0])) | (a[1] & b[1]);
// assign ans[2] = C[1] ^ (a[2] ^ b[2]);
// assign C[2] = ((a[2] | b[2]) & C[1]) | (a[2] & b[2]);
assign ans[2] = (((a[1] | b[1]) & (a[0] & b[0])) | (a[1] & b[1])) ^ (a[2] ^ b[2]);
assign C[2] = ((a[2] | b[2]) & (((a[1] | b[1]) & (a[0] & b[0])) | (a[1] & b[1]))) | (a[2] & b[2]);
// assign ans[3] = C[2] ^ (a[3] ^ b[3]);
// assign C[3] = ((a[3] | b[3]) & C[2]) | (a[3] & b[3]);
assign ans[3] = ((a[2] | b[2]) & (((a[1] | b[1]) & (a[0] & b[0])) | (a[1] & b[1]))) | (a[2] & b[2]) ^ (a[3] ^ b[3]);
assign C[3] = ((a[3] | b[3]) & ((a[2] | b[2]) & (((a[1] | b[1]) & (a[0] & b[0])) | (a[1] & b[1]))) | (a[2] & b[2])) | (a[3] & b[3]);
//如果你需要八位的加法器,把下面的注释去掉
// assign ans[4] = C[3] ^ (a[4] ^ b[4]);
// assign C[4] = ((a[4] | b[4]) & C[3]) | (a[4] & b[4]);
// assign ans[5] = C[4] ^ (a[5] ^ b[5]);
// assign C[5] = ((a[5] | b[5]) & C[4]) | (a[5] & b[5]);
// assign ans[6] = C[5] ^ (a[6] ^ b[6]);
// assign C[6] = ((a[6] | b[6]) & C[5]) | (a[6] & b[6]);
// assign ans[7] = C[6] ^ (a[7] ^ b[7]);
// assign C[7] = ((a[7] | b[7]) & C[6]) | (a[7] & b[7]);
endmodule
8. 测试代码
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include "verilated_vcd_c.h" //可选,如果要导出vcd则需要加上
#include "Vtop.h" //.v -> .h
#include <iostream>
#include <bitset>
vluint64_t main_time = 0; //initial 仿真时间
double sc_time_stamp()
{
return main_time;
}
int main(int argc, char **argv)
{
Verilated::commandArgs(argc, argv);
Verilated::traceEverOn(true); //导出vcd波形需要加此语句
VerilatedVcdC* tfp = new VerilatedVcdC; //导出vcd波形需要加此语句
Vtop *top = new Vtop("top"); //调用VShuang.h里面的IO struct
top->trace(tfp, 0);
tfp->open("wave.vcd"); //打开vcd
int a = 1;
int b = 0;
int c = 0;
while (sc_time_stamp() < 7 && !Verilated::gotFinish()) { //控制仿真时间
top->a = a; //激励控制
top->b = b;
top->c = c;
top->eval(); //计算输出
std::cout<<a<<" "<<b<<" "<<std::bitset<4>(top->ans)<<" ";
printf("%d\n", top->ans);
tfp->dump(main_time); //dump wave
main_time++; //推动仿真时间
a++;//向后产生加数,你自己random产生测试数据也行
b++;
}
top->final();
tfp->close();
delete top;
return 0;
}
9. 输出
左边两个是加数,中间的是二进制,后面的是十进制表示:
1 0 0001 1
2 1 0011 3
3 2 0101 5
4 3 0111 7
5 4 1001 9
6 5 1011 11
7 6 1101 13
10. 编译命令
文件名为 top.v main.cpp
verilator -Wno-fatal top.v main.cpp --top-module top --cc --trace --exe #编译.v文件
make -C obj_dir -f ./Vtop.mk Vtop #编译cpp
./obj_dir/Vtop #运行
gtkwave wave.vcd #查看vcd波形
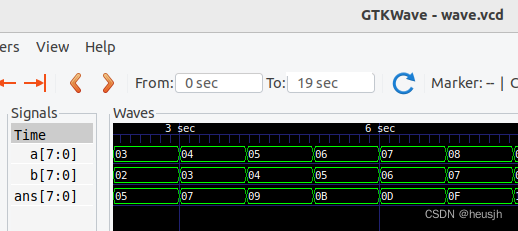
后记:1.一开始忘了卡诺图每一个相邻项只能变一个值,写成了00 01 10 11,怎么化简也化不出来,后来才发现,真的是,才疏学浅。 2.这玩意还写了半天,真的是很不熟练。 3.本例仅供学习超前进位加法器原理使用,实际编程直接+就完事了,verilog内置的肯定比咱写的垃圾加法器优化要好。
